The Question
In the last post I mentioned a problem that I’d discussed with Anders, who had kindly written to me after following the blog for a while. This was the problem:
Like many countries, Denmark has its own version of the TV quiz show Who Wants to be a Millionaire?. The format and rules are identical to the UK version, but the prize money is in Danish Kroner. Anyway, a while back on the 22 February, 2022, one contestant, Balder Kringelbach, got to the final question, which was as follows:
Which of these Danish comedy movies premiered first?
A) Sover Dolly på Ryggen
B) Klassefesten
C) Blå Mænd
D) Superclasico
The contestant, Balder Kringelbach, was sure that movie C was older than A or B but didn’t know anything about movie D. Balder regards this choice as a 50-50 ‘coin-flip’, so chose not to play, meaning he kept the half a million Kroner he’d already accumulated, rather than risking it for the full million.
However, Anders argued that Balder’s chances of winning were considerably better than that. His reasoning was that there are 24 possible arrangements of the movies in chronological order. But if we limit ourselves to those where movie C comes after A and B, the only remaining arrangements are these:
A B D C
A D B C
B A D C
B D A C
D A B C
D B A C
B A C D
A B C D
Each of these is equally likely and in 6 of them C come after D. The actual probability that movie C is oldest is therefore 6/8 or 3/4. These are very favourable odds for an evens-priced bet and it was therefore in Balder’s interests to take the question on with the answer C.
My question in last month’s post was whether this argument is correct or not? There are at least 3 possible answers that I’ll explain below.
Answer 1: Anders’ argument is correct.
Assuming the 24 combinations are genuinely equally likely, and that the contestant really has no information other than that movie C is older than A and B, Anders’ reasoning is completely right. In fact, stated this way, the problem is very similar to a classical ‘apparent paradox’ in probability, known as the Monty Hall Problem.
There are different variations, but the standard version describes a game show in which a contestant has to choose between 3 closed doors. Behind one of the doors is a car; behind the others there is a goat. The contestant has to guess which door is hiding the car. But having made a guess – let’s say door A – the host shows the contestant that another of the doors – let’s say door B – is not hiding the car. The contestant is then asked whether she would like to stick with door A or change to door C. Many people’s instincts are that since the only available information is that the car is not behind door B, it’s 50-50 whether it’s behind door A or C. There’s therefore no advantage in switching to door C and the contestant might just as well stick with door A.
But this turns out to be wrong. The additional information that the car is not behind door B actually reduces the chances that it’s behind door A to 1/3 and raises the chance that it’s behind door C to 2/3. This being so, the contestant would improve their chances of winning by switching to door C.
There are different ways of showing this result. One simple explanation is this. Initially, the chances that the contestant had chosen the correct door were 1/3. Having made that choice – whatever it is – the show’s host would always be able to look behind the other two doors and then open one that is not hiding the car. Given that’s the case, the extra information gained by seeing that door B does not contain the car must be irrelevant so far as the probability that the car is behind door A is concerned. The probability that door A is hiding the car must therefore remain at 1/3, and since we now know the car is not behind door B, the probability it’s behind door C must be 2/3.
To my mind it’s beautiful that the movie question, seen this way, turns out to be a real-life illustration of the Monty Hall problem. The analogy can be seen more easily if we simplify the movie question so there are just three possible answers, now relabelled to emphasise the analogy:
A) Superclasico
B) Sover Dolly på Ryggen
C) Blå Mænd
The contestant initially considers Superclasico as the oldest movie and knows that Blå Mænd is older than Sover Dolly på Ryggen. This is equivalent to initially choosing Door A and being told that the prize is not behind door B. Given this information, the chance that Blå Mænd is the oldest movie is not 50-50 but 2/3, by exactly the same logic as used in the Monty Hall problem, and the contestant has a greater chance of winning by switching to Blå Mænd. The extension to four possible answers follows by similar logic, and again the contestant has a better chance of winning by answering with Blå Mænd. The probability of winning in this case is 3/4, as the above logic correctly showed.
Answer 2: Anders’ argument is incorrect (sort of).
Anders’ argument is formally correct, but relies on a very strict interpretation of the contestant’s knowledge and behaviour. In reality, things are likely to be slightly different. For example, the contestant believes that Blå Mænd is older than Sover Dolly på Ryggen and Klassefesten. But is that because he knows the latter two movies are very recent or because he knows Blå Mænd is very old? If it’s the former, then it’s quite plausible that Superclasico is older still; if it’s the latter, then it’s less likely. In other words, what Balder Kringelbach actually knows about the movies is unlikely to be limited to the information that was used in the ‘Monty Hall’ argument, and his chances of winning with answer C will actually depend on what that knowledge is.
We can illustrate this by making some simple assumptions. Suppose Balder is prepared to give an identical probability distribution to the age of movies C and D, perhaps something like the following:
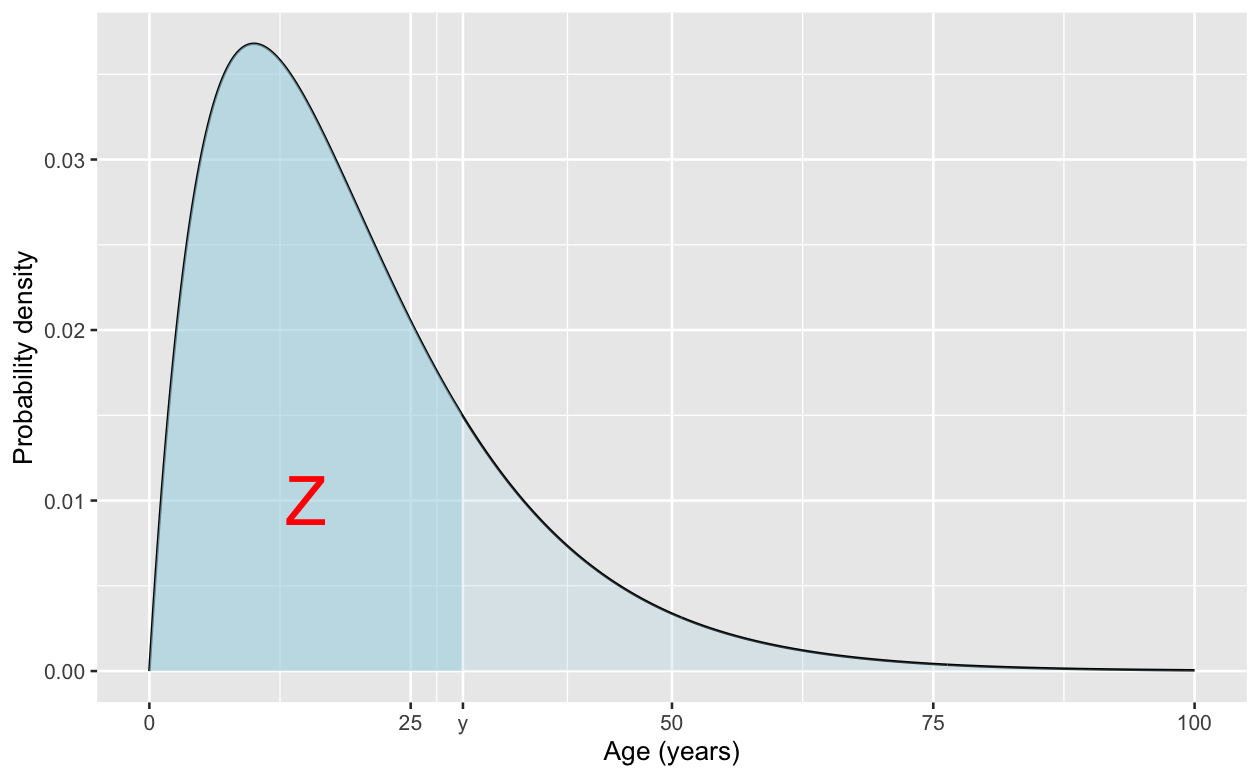
In other words, he believes each movie is definitely less than 100 years old; almost certainly less than 50 years old; and most likely less than 25 years old. But now presented with the comparison with the other movies, he realises that movie C is older than movies A and B. He also knows that one of those films is y years old; so he actually now realises that movie C is at least y years old; i.e. somewhere to the right of y in the above figure. So the probability that movie C is oldest is actually the probability that movie C is older than movie D given that we know it’s at least y years old.It’s then not too difficult to show that this probability is
p = 1/2 + Z/2
where Z is the area shown in the graph, corresponding to the unconditional probability that movie C is less than y years old.
When y is close to zero, the contestant only knows that Blå Mænd is not a very recent movie, and this probability is close to 1/2. But as y increases, meaning that Balder knows that Blå Mænd is an increasingly old movie, the probability it’s an older movie than Superclasico increases towards 1.
In summary, if this is a reasonable way to represent Balder’s relative knowledge about the movie ages, his chances of winning will be anywhere between 1/2 and 1 depending on the value of y. Moreover, the answer of 3/4 provided by Anders’ logic sits exactly in the middle of this range of possible answers.
Answer 3: Anders’ argument is correct, but the contestant made the right choice anyway.
For argument’s sake, let’s suppose Anders’ argument is correct, so Balder’s true probability of winning if he went ahead and gave C as the answer was 3/4. This means his expected winnings with this strategy in millions of Kroner are:
3/4 x (1/2) + 1/4 x (-1/2) = 1/4.
So, if Balder’s aim was to maximise his expected wealth, he should have taken the question on. But this assumes it’s a zero-sum game in terms of Balder’s happiness; i.e. that he’s equally happy to win half a million Kroner as he is unhappy to lose it. On this terms, Answer 1 suggests that the contestant should have taken the question on.
However, as we discussed in a previous post, much of economic theory is based on the notion that winning and losing are not symmetric outcomes in term’s of a person’s happiness. In this particular case, having already accumulated half a million Kroner from the previous questions, Balder’ happiness level might have gone down a lot more by losing that money than they would have gone up by doubling it. In other words, despite the odds being in Balder’s favour and the price of the bet being evens, his decision to stop may well have been consistent with maximising his expected happiness by the end of the show.
Postscript
In the event, Blå Mænd was revealed to have premiered first, and Balder would have won the whole million if he’d gone with answer C. Nonetheless, he said at the end of the show:
Quitting the game was the correct decision. It is a waste to lose that much money on something that is a 50/50 gamble. I would be shitting on a lot of people if I did that.
No regrets, then. But what if it he’d believed it was a 75/25 gamble? Would taking that bet on have still been shitting on a lot of people?
