This is a follow-up to the previous blog post which described a series of puzzles based on a description of the recruitment process at Smartodds. Of course, the description was just a L.I.E. to give a context to the puzzles.
The puzzles themselves are based on a recent post in the series of Guardian Maths Puzzles by Alex Bellos, though Alex himself references that the puzzle has appeared previously in various places. Alex’s description and solution of the puzzle are interesting, though I found it even more interesting reading both the replies of readers to his column and the discussion given in the alternative versions of the puzzle he also references. It’s surprising how many different ways this puzzle can be viewed and solved. I’m giving my own take on things here, though you may find any of the alternative explanations available to work better for you.
Alex’s version of the puzzle – with a different background story – is equivalent to Part 2 in the version I posted. I hoped that the inclusion of Part 1 would make the puzzle easier to explain, but perhaps also lead you to the wrong answer for Part 2. I also hoped that the inclusion of Part 3 might lead you to question your answer to Part 2 if indeed you had applied a false logic in answering it.
First, the answers to Parts 1 and 2:
Part 1: Bill and Ted are both equally likely to get the job.
Part 2: Thelma is more likely to get the job than Louise.
The puzzle – I believe – tempts you into a false interpretation of what randomness in the allocation of the letters implies. The temptation is to think:
1. The letters are placed randomly in the envelopes.
2. By symmetry, all possible orderings for opening the envelopes must be equally good.
Therefore
3. Bill and Ted (and Thelma and Louise) must be equally likely to get the job.
Statements1 and 2 are correct, but to conclude Statement 3 from those assumptions is incorrect. Nonetheless, and what might lure you into a false argument for Statement 2, Statement 3 does turn out to be true in the case of Bill and Ted, though a different logic is required to prove it. Statement 3 is false in the case of Thelma and Louise.

To see why Bill and Ted are equally likely to get the job, I’ve annotated the figure from the post with the name of the person who will first open each envelope. If there’s no name it’s because that envelope is opened by Bill and Ted simultaneously. For example, envelope A is opened simultaneously by Bill and Ted (in the first round); envelope B is opened first by Bill (in the second round); envelope F is opened first by Ted (also in the second round). And so on.
Since the job is awarded to the person who finds the “you’re hired” message first, there are 6 scenarios where Bill wins (message in envelope B, C, D, E, I or J), 6 scenarios where Ted wins (message in envelope F, G, K, L, M or N) and 3 scenarios where neither candidate is awarded the job (message in envelope A, H or O). Furthermore, the “you’re hired” message was allocated randomly among the envelopes and is therefore equally likely to be in each, so there’s a 6/15 chance Bill gets the job, a 6/15 chance Ted gets the job and a 3/15 chance neither candidate gets it. It follows that Bill and Ted are equally likely to be offered the job.
The same logic applies to Thelma and Louise with one exception. Since Thelma and Louise adopt the same order of opening the envelopes as Bill and Ted respectively, the diagram above is still valid, with Thelma taking the place of Bill and Louise taking the place of Ted. So, Thelma will get the job if any of the envelopes B, C, D, E, I or J is the first to contain a “you’re hired” message, while Louise will get the job if F, G, K, L, M or N is the first envelope to contain such a message. What makes things different is that since two messages have been randomly allocated in envelopes, the probabilities of these events are no longer equal.
To see why that’s the case, consider an easier situation where there are just three envelopes labelled A, B, C and we randomly place messages in 2 of them. We then open the envelopes in the order A, B, C and identify the first envelope that contains a hidden message. There are 3 possible pairings for the placement of the messages – (A, B), (A, C) and (B,C). In 2 of these the first time a message is found is in envelope A, on 1 occasion it’s in B and on no occasions it’s it in C. So, although the 2 messages were allocated randomly, the probabilities of the first opened message are skewed towards the start of the sequence in which the envelopes are opened: there’s a 2/3 probability it’s in A and a 1/3 probability it’s in B.
It’s not too difficult to generalise this argument to the situation where the two messages are randomly allocated among 15 envelopes. By the same logic, the probabilities are skewed towards the front end of the sequence in which the envelopes are opened. Now if you look back at the envelopes which would lead to either Thelma or Louise getting the job, B and F would be opened in round 2, C and K in round 3, E and G in round 5 and I and M in round 9. So these scenarios will have the same probability for either candidate. However, Thelma also gets the job if the message is in envelopes D or J, which would be opened in rounds 4 and 10 respectively. On the other hand, Louise gets the job if the message is in envelopes L or N which would be opened in rounds 6 and 12 . In these cases the envelopes which would lead to Thelma getting the job are opened earlier than that that would lead to Louise getting the job. And because of the skew in probabilities towards the start of the sequence, it follows that Thelma’s probability of finding a “you’re hired” message first is greater than that of Louise’s, so Thelma is more likely than Louise to get the job.
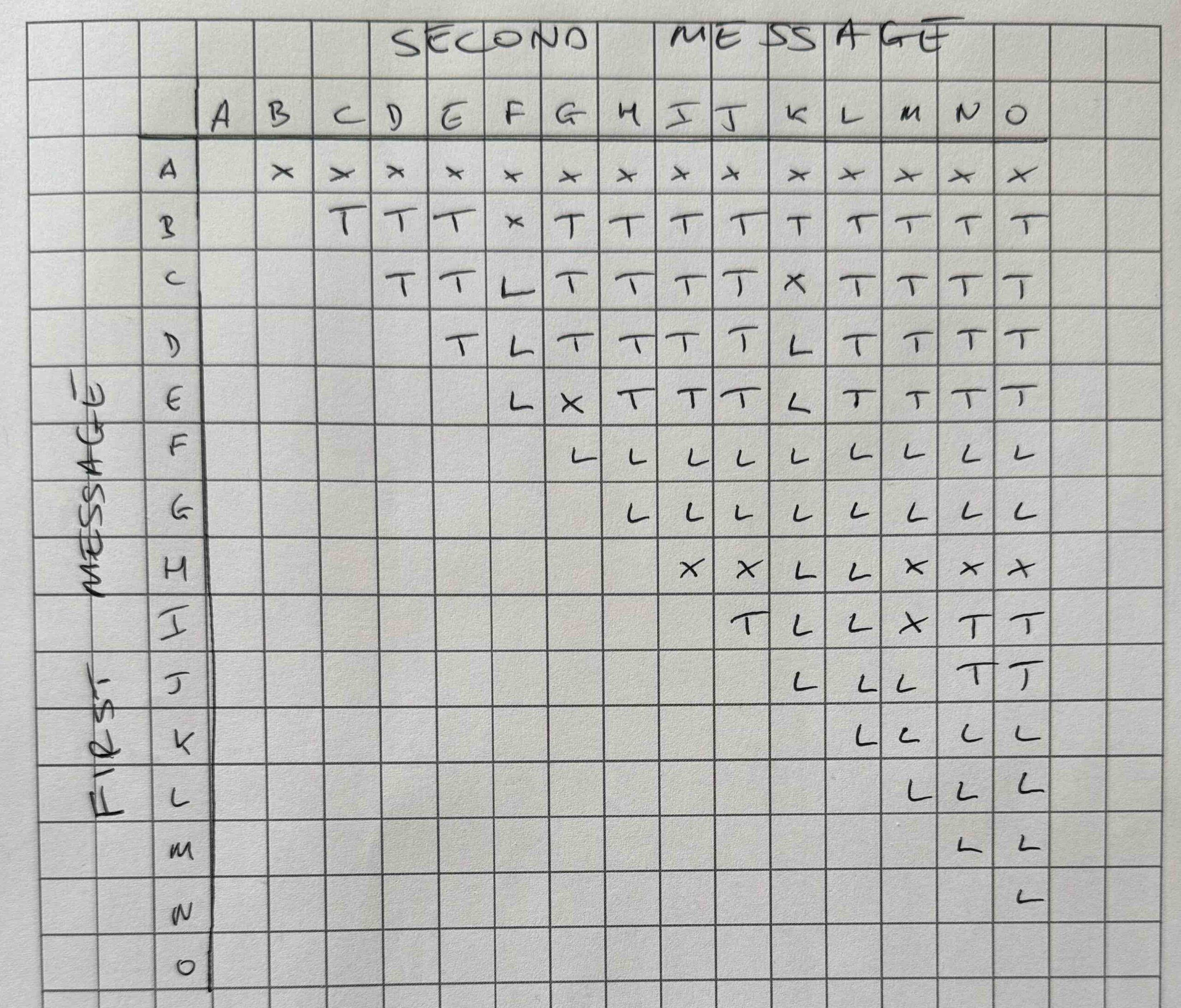
Having said all that, I found it difficult using this argument to actually calculate the probabilities of either Thelma or Louise getting the job. In the end I just listed all of the possible pairings for the “your hired” message – (A, B), (A, C), etc. – each of which is equally likely due to the random allocation. These pairings are shown in the figure above. I then identified the outcome for each combination – e.g. anything with an A will result in both Thelma and Louise finding the message on the first round – and then simply summed the combinations which led to the different outcomes. There are 105 pairs in total, of which 23 lead to neither candidate getting the job, 43 in which Thelma gets the job and 39 where Louise gets the job. So Thelma gets the job with probability 43/105, while Louise gets it with probability 39/105. Although this shows that Thelma is more likely than Louise to get the job, it’s hard from these calculations to see exactly why that should be the case.
As I wrote at the start of the post, the fact that Thelma and Louise have different probabilities of getting the job might seem counter-intuitive. But part 3 is intended to help with the intuition. Nancy knows that Sid has gone for an alphabetical ordering, A to O. Suppose she decided to make exactly the same choice. Then she and Sid would be bound to find the “you’re hired” message simultaneously and neither she nor Sid would get the job. This at least shows that the choice of order does affect Nancy’ chances of getting the job, though with this choice she guarantees she doesn’t get the job.
What Nancy could do though is choose this sequence: B, C, D, through to O, followed by A. In this case Nancy opens every letter before Sid does, except for the letter A. So, Nancy is bound to get the job unless the “you’re hired” message happened to be in envelope A. Then, since we’ve returned to the situation where there’s just one such message randomly distributed, this means that Nancy’s probability of getting the job is 14/15, while Sid’s is just 1/15.
Now, why does the basic logic I suggested at the start of this post fail, even – as we’ve now seen in part 3 – in the case where just one letter is hidden in the envelopes? It’s true that the letter is placed randomly among the envelopes, and equally true that any chosen sequence is just as good as any other. However, it’s not true that all strategies are equally good against all others.
Consider a much simpler game – Rock, Paper, Scissors. Paper beats Rock, Rock beats Scissors, Scissors beats Paper. So, unless you have insight as to what your opponent will play, all choices work equally well. You’ll win, lose or draw, each with probability 1/3. But once your opponent has made a choice, some strategies are better than others. And if you overheard your opponent make their choice in a conference call, you’d know exactly what play to make. The envelope scenario still involves some randomness, so Nancy couldn’t force a win, but with the right choice she could get her win probability up to 14/15.
So, even with a single letter, the “logic” that all players are equally likely to win once they’ve made their choices is wrong. They are equally likely to win until the choices are known, but once they are known, some choices will be superior to others. It’s simply an “exceptional case” that Bill and Ted had made choices that gave them equal probabilities of getting the job. And if you applied the same logic to the two letter case, it would be wrong.
Incidentally, Gil Kalai’s discussion of this problem included a Twitter poll. This relates to Part 2 in my version of the problem, with “Thelma” and “Louise” replaced by “Andrew” and “Barbara”. Re-interpreting the results in the context of my version of the puzzle, roughly 41% of respondents in the poll thought Thelma more likely to get the job, 14% thought Louise more likely, and 45% thought they were equally likely. So if you also came to that conclusion, you’re definitely not alone and it’s interesting how randomness can lead us to false conclusions in quite simple scenarios.
A final thing – though this post is related to issues of games, probability and chance, does it have any direct relevance to the sort of things we do at Smartodds? I believe it does. Many standard models for the analysis of sport data are implicitly (or explicitly) designed on the idea of team ratings. This includes the famous/infamous Dixon and Coles paper for modelling football scores. The idea in all these models is to capture a team’s strength – or rating – by some kind of quantity to be estimated and then to calculate the probability of one team beating another as a function of the difference in their ratings. But this leads to a transitive rule for win probabilities – if team A has a higher rating than team B, and team B has a higher rating than Team C, then when A plays B, A is more likely to win, when B plays C, B is more likely to win, and when A plays C, A is more likely to win. This might be an accurate assumption. But what if team A’s style of play mean they are likely to win against B; team B’s style of play mean they are more likely to win against C; and C’s style of play mean they are more likely to win against A. This is exactly like the L.I.E. scenario, or indeed Rock-Paper-Scissors. In these scenarios the mapping of Team ability to win probabilities is more nuanced and a simple ratings based model is bound not to be entirely accurate.
Postsript 1
Alex Bellos has recently published a new book of puzzles. I haven’t read it, but based on his regular column in the Guardian it’s likely to include puzzles that are challenging and fun.
Postscript 2
Thanks to the several of you who wrote to me to discuss solutions to this puzzle. No one fell into the trap I described above, and everyone made good progress with parts 1 and 3, though part 2 was sometimes found more challenging. A special shout out to Mike S who wrote a search algorithm to find the optimal strategy for opening the envelopes based on assumptions defining a class of orders the other candidate might adopt in opening their set of envelopes.
