Sticky Problem 1
Q: What’s brown and sticky?
Scroll down for answer:
|
|
|
|
|
|
|
|
|
|
A: A stick.
Ok, terrible. So how about this?
Sticky Problem 2
If I take a stick and break it randomly in 2 places, what’s the probability that I can form a triangle with the 3 broken pieces?
For example, if the stick is 10 cm long and it gets broken into pieces of length 7cm, 2cm and 1cm, then it’s impossible to make a triangle. That’s because the sum of the two shortest pieces is less than the length of the longest piece.
On the other hand, if the broken pieces are of length 4cm, 3cm and 3cm, then a triangle is easily constructed: 
What’s the Point?
There are two reasons why I’m asking this question. The first is because we make decisions that depend on chance events all the time.
For example:
- I’ll walk to work unless I think it more likely than not to rain, in which case I’ll take the bus. Given the weather forecast and the current weather conditions, I therefore have to judge whether the chance of rain is greater than 50%.
- I’m trying to sell something on eBay for£50, and I receive an offer of £40. Should I accept the offer or wait and hope for a higher bid, with the risk of losing the current offer? This will depend on what I believe the chances are of getting a higher offer.
- What shall I do tonight? I could stay in or go out with my friends. I’ll have a better time with my friends unless I drink a bit too much and end up with a headache. What are the chances of drinking too much if I do decide to go out?
Every day we all make hundreds of similar decisions, where we are required to make an instinctive probability judgements. But how good are we at doing this?
Let’s see with the triangle problem. I’d like you to guesstimate the answer. You can either mail me your answer directly, or fill in the (anonymous) survey form here.
If you think it very likely that a triangle can be made from the three randomly broken pieces, you’ll choose a probability close to 100%. If you think it unlikely, you’ll choose a probability close to 0. And the more likely you think it is, the bigger the probability you’ll give.
I’ll update this post in a couple of weeks with a summary of responses. Obviously, please don’t Google the problem, at least until you’ve sent me your own answer.
The second reason for posting this question is that the theoretical solution I’ve seen is quite beautiful and I’d like to share it with you. So when I update the post, I’ll also include this solution. If you’re mathematically minded and would like to send me your own solution, I’d be very happy to receive that as well.
But that’s really a secondary thing: it’s the collective guesses to this problem that are much more interesting, and the more replies received, the more interesting the results are likely to be, so please take a couple of minutes to reply if you can.
Solution
The answer to the stick problem turns out to be 1/4. There are different ways of proving it, but one solution, which is both elegant and reasonably intuitive, uses a connection between geometry and probability. It’s not too complicated, but requires more sophistication than is appropriate to include in this post, so I’ve written a short note containing the proof that you can find here.
But as I wrote above, it’s the estimates received that are much more interesting, since they tell us something about our collective ability at making probability judgements.
At the time of writing, I’ve received a total of 16 responses. The following histogram gives a broad picture of the estimates made:
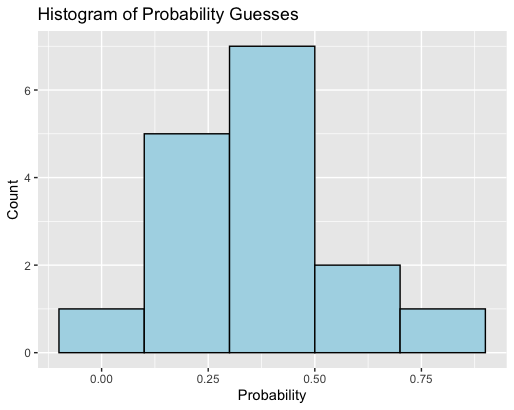
As you can see, there’s a fairly wide spread of answers, but the average – which is 0.41 – is not too bad an estimate of the true value of 0.25. Actually, I should give a shout out to Fabian, Louis and Paul W who each sent me detailed proofs – different from the one I’ve provided above – that the answer is 0.25. If I remove their responses, leaving just the answers based on guesswork, the average goes up to about 0.44, which is arguably still not bad as a collective average guess. Nonetheless, this was a fairly easy-to-visualise problem and yet the collective responses were highly variable.
Anyway, this kind of approach is often used for incorporating expert opinion into statistical analyses. A number of experts – “you” in this case – might be asked their best guess about something – the probability of making a triangle, here – with the estimates being combined, as per the histogram above. This is a combined-expert probability distribution, which can be thought of as a “Prior” probability assessment. In experimental situations, as data become available, there’s an updating procedure based on Bayes’ Theorem that leads to a “Posterior” distribution, which correctly balances the different information provided by the experts and the data.
I should also give a special shout out to Benoit and Gavin M, who both asked ChatGPT to provide a solution to the stick problem. In Benoit’s conversation, ChatGPT confused itself by requiring the total length of the broken pieces of stick to be less than the original, but it did conclude that the probability has to be less than 1,
The conversation with Gavin was a bit more detailed and precise, and ChatGPT noted – as in my discussion above – that if the broken sticks were of length (s, t, u) , then the probability we are looking for is
P( s+t > u, s + u > t, t + u > s)
This is correct, since it’s the probability that the sum of every pair of sides is greater than the length of the third side. Actually, I find it remarkable that ChatGPT was able to formalise the solution mathematically in this way.
Unfortunately, ChatGPT then made a schoolboy error and factorised the above probability as
P( s+t > u) P( s + u > t) P( t + u > s)
which is wrong since the events are not independent. ChatGPT also said these probabilities cannot be found, which is also wrong as long as you interpret the random breaking of a stick to mean that it is equally likely to be broken at any point along its length, as I had intended.
Brilliant anyway.
