Introduction
I wish I could take credit for the title of this post, but I can’t. It’s the title of an article in The Economist that discusses the results of a staking experiment, which we recently replicated at Smartodds. Details of the experiment, together with a discussion of the theory of optimal staking strategies, are given in my previous post here.
The game consisted of a sequence of virtual coin tosses, with bets offered at even money, though Heads and Tails had unequal win probabilities of 60% and 40% respectively. This meant a bet of Heads at each round was a positive value bet, but the more interesting issue was that of stake sizes. Participants had a virtual initial bank of $25 and were also told there was an upper limit to the bank which, although they didn’t know it, was actually $250.
The conventional approach to staking in games of this type is the Kelly Criterion, which amounts to:
- Always betting a constant proportion of the current bank size;
- Setting the proportion based on the price and win probability of the bet.
With a price of evens and a 60% win probability for Heads, the Kelly Criterion implies betting Heads each round at a stake that’s always 20% of the current bank. However, the fact that the bank had an unknown upper limit meant that the conditions which imply Kelly to be optimal, do not strictly apply. Moreover, Kelly is just one possible theoretical approach, as discussed fully in the previous post. As such, there are no absolute right and wrong strategies and it’s of genuine interest to look at the range of approaches adopted and the results they led to.
What Approaches Did Smartodds Participants Take?
The table below summarise the strategies adopted by Smartodds participants. Most individuals appear more than once: for example, someone who always bet Heads and followed the Kelly criterion exactly, will show up in both rows 1 and 4. By contrast, not everyone provided full information – for example, someone may have always bet Heads without actually saying so.
| Strategy | Frequency |
|---|---|
| Always Bet Heads | 18 |
| 60/40 H/T Bets | 1 |
| H/T Chosen at Random | 1 |
| Exact Kelly | 9 |
| Super-Kelly | 4 |
| Sub-Kelly | 1 |
| Bespoke Kelly | 2 |
| Constant Stake | 1 |
| Lower Stake When Betting Tails | 1 |
| Trial Low Stakes | 1 |
| Double Stake After a Loss | 1 |
| Double Stake After a Win | 1 |
| Gradual Doubling of Stake | 4 |
| Gradual Increase of Stake | 2 |
| All-in From Start | 1 |
| All-in Eventually | 5 |
| High-Frequency Betting | 3 |
| Lucky Accident | 3 |
Some further explanations:
- Exact application of the Kelly Criterion implies betting 20% of the current bank on each coin toss. Some people applied the Kelly rule with something other than 20%: I’ve called these ‘super-‘ and ‘sub-‘ Kelly for proportions greater than and less than 20% respectively. ‘Bespoke’ was a further variation on ‘super’ and ‘sub’.
- ‘Trial Low Stakes’ means stakes were initially kept low while testing whether the information I’d given about Heads/Tails having a 60/40 probability split was accurate or not.
- ‘High-frequency Betting’ counts participants who explicitly mentioned that they aimed to make as many bets as possible within the 30 minutes available, or before they hit the upper or lower limit.
- ‘Lucky Accident’ counts participants who mentioned that they hit the wrong key, or made some other mistake in execution, but got lucky. (Nobody admitted to unlucky accidents.)
To try to summarise this table:
- The first point to note is that the majority of players – at least among those who provided information on their choice of bets – always played Heads. As explained in the previous post, regardless of staking strategy, this is always the right thing to do. At least, it is if the information given to players is correct. One participant ran a number of rounds with a low stake to check whether the 60% Heads probability was likely to be correct, before adopting any kind of strategy based on the fact that it was. This is a robust strategy that factors in the possibility of mis-information, though a bit wasteful if that information is trustworthy. Such trade-offs between robustness and efficiency are common in statistical decision-making.
- In terms of staking strategies, the majority of participants adopted Kelly in one form or another. Playing Kelly with a lower than optimal stake is safe, and is arguably a superior strategy, given that there is an upper limit to the bank. Playing super-Kelly is also reasonable up to a point, but if the proportion staked is too high, a sequence of unlucky results will have a large impact on the bank and risks dragging the total towards zero. See the previous post for discussion of this issue. Several participants ended up with zero by precisely this route.
- As an alternative, several people doubled their stake dependent on a win or a loss, Increasing stakes after a loss is definitely the wrong thing to do. Arbitrarily increasing stakes after a win is also unjustified, except in so much as Kelly would also lead to some increase in stake size after a win. Not explicitly because of the win, but because the bank itself has increased. However, increasing stake sizes by as much as 100% after a win is very risky for the same reason that too large a proportion within the Kelly criterion is risky.
- Several people, even among those who knew about Kelly and were applying that criterion, lost interest or patience and just went all-in at some point.And often lost everything as a result.
- Just one person went all-in from the very first round, and lost. (See below).
- Several people mentioned that since a bet on Heads was a positive value bet, and in light of the fact that there was a limit on how much could be won anyway, it was reasonable to minimise risk by keeping stakes low and compensating by executing bets as quickly as possible. This is entirely sensible, though had the upper limit been much higher than $250, it may have required an unfeasible number of rounds to reach that limit with very low stakes. A couple of participants experimented with bots to enable fast execution and circumvent this problem.
- Finally, several people reported getting lucky by hitting the wrong key or entering the wrong amount.
I haven’t done a careful analysis of how results varied by strategy, but participants who adopted Kelly consistently with a staking proportion of 20% or lower almost always reached the maximum bank of $250. Just one such player failed to reach the upper limit, but still made a healthy profit. Those who adopted Kelly with a higher proportion than 20% also usually reached $250, though in some cases, especially where the staking proportion was much higher than 20%, this strategy led to a final bank of zero. This is exactly what the theory suggests.
Other strategies had variable results. Sometimes players got lucky, but riskier strategies generally led to lower winnings, often zero. And several of the players who got bored and went all-in, lost everything, even though they may have played an optimal strategy up to that point. A system requires constant application, and patience is a virtue.
Comparison With Results From Original Experiment
One reason for carrying out this experiment was to see how participants connected to Smartodds – a company closely involved with betting on sports markets – would fare relative to participants from a wider population. In the original experiment there were 61 participants who were “largely comprised of college-age students in economics and finance and young professionals at finance firms.” So, not gamblers exactly, but people who were likely to know the basics about risk, investment and pricing. By contrast, many of the people connected to Smartodds have direct experience of gambling markets.
A summary of the results obtained by the Smartodds participants is given in the following graph: the horizontal axis corresponds to the number of rounds played until the game was timed out or the upper or lower limits was reached. The vertical axis is the final bank size.
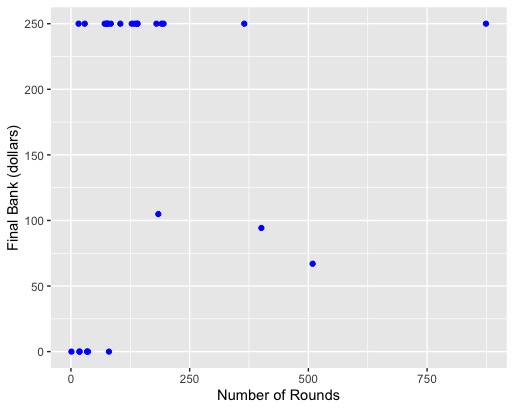
As you can see, almost all participants hit the lower limit of zero or the upper limit of $250. They’re a bit hidden due to overlap, but there are actually a total of 7 participants with a final bank of $0 and 17 with $250. The number of rounds played ranged between 1 and 874 – both actually quite remarkable numbers given the 30-minute time limit.
A comparison of headline results with those of the original experiment is given in the following table:
| Original | Smartodds | |
|---|---|---|
| Number of Participants | 61 | 27 |
| Won the Maximum | 21% | 63% |
| Lost Money | 33% | 26% |
| Lost Everything | 28% | 26% |
| Average Winnings | $91.40 | $167.30 |
So, notwithstanding the smaller sample size, the proportion of individuals at Smartodds who hit the upper limit of $250 was three times as great. On the other hand, the proportion of participants who lost the whole bank was roughly the same in both populations (28% versus 26%). Another contrast: nobody lost money in the Smartodds experiment, except those who lost everything. And the average final bank for Smartodds participants was close to double that of the original experiment.
One of the main conclusions of the published report on this experiment was that the Kelly Criterion was much less well-known, even among students in a finance/investment environment, than one might hope or expect. The authors reported that only 5 of the 61 participants had heard of the Kelly Criterion, and not all of those had correctly applied it. By comparison, a significant proportion of the Smartodds participants knew about the Kelly Criterion, or had sufficient intuition to base their strategy on something along those lines. Either way, the results demonstrate that a systematic approach to staking is important, and that Smartodds participants generally have the requisite knowledge or intuition.
Conclusions
Happily, I think it fair to conclude that Smartodds participants proved to be, on average, less irrational tossers than the tossers of the original experiment.
Players who followed something like the Kelly Criterion of always betting 20% of current bank generally fared well, and this was the dominant approach among Smartodds participants.
Finally, I’m very grateful to everyone who participated and happy that, from the feedback I received, most people who took part found it to be a thought-provoking and rewarding exercise.
Postscript
When I invited people to participate in this experiment I promised I wouldn’t discuss individual approaches or results. With the permission of the relevant individuals, I’d like to make a small exception to that rule.
Two of the participants were father and son. If you know much about Smartodds, you can probably guess who they are. For argument’s sake let’s call them Nity and Arjun. I’m immensely proud that both Nity and Arjun thought really carefully about the statistical principles involved in playing this game, and determined their strategies accordingly. It’s also hugely satisfying that despite their genetic overlap, they came to completely opposite conclusions about what strategy to adopt.
Nity realised that he’d maximise his expected winnings by staking his entire bank on Heads every time. But as discussed in the previous post, although this strategy maximises winnings, it also leads to a bank of $0 with very high probability. But still, it is the strategy that generates maximum expected profit, and Nity realised that and went straight in with a $25 bet. And lost. Slightly against the rules, he tried again with the same strategy. And lost. Which was pretty unlucky, to be honest, but he was very likely to lose with that strategy at some point before hitting the $250 upper limit, so at least he saved a bit of time with the quick losses.
Arjun, on the other hand, realised that it made sense to bet a constant proportion of the bank, though he didn’t know about Kelly and so didn’t know what the ‘correct’ proportion should be. He guessed 60%, which is actually a bit on the high side. If you look at the previous post, you’ll see that size of bet actually carries a reasonable risk of losing money. But Arjun got lucky and hit the maximum $250 anyway. He also realised that it would have been safer to make bets with a lower stake but at a higher frequency, and so experimented with building a bot to carry out that execution.
So, both brilliantly thought-out strategies, each of which can be justified in terms of maximising a certain utility within a decision-theoretic framework. And both led to the game limit being achieved. Just, in Nity’s case, it was a limit of zero after a single round.
