Introduction
Being able to count the number of different ways events can occur is a fundamental skill that’s necessary for many types of probability and Statistics calculations.
Let’s do a chess example.Two friends. Boris and Magnus, agree to play a sequence of 9 chess matches. Magnus wins each match with probability 0.4. What’s the probability he wins 6 of the 9 matches?
If the probability Magnus wins a match is 0.4, then the probability he’ll not win a match – which could be a draw or a loss – is 0.6. So, by basic probability rules, the probability Magnus wins a specific set of 6 matches (and therefore also lose a specific set of 3 matches) is
(0.4)^6 \times (0.6)^3
But, it doesn’t matter which set of 6 matches he wins, so we have to multiply this number by the number of different ways he could win those 6 matches. For example, he could win the first 6, then lose the next 3. Or he could lose the first 3, then win the next 6. And so on.
So, we’re looking for the number of rearrangements of the letters in the sequence
M M M M M M B B B
The number of arrangements of 9 distinct letters is given by
9! = 9 \times 8 \times 7 \times 6 \times 5 \times 4\times 3\times 2\times 1 = 362880
That’s because there are 9 choices for the first letter. For each of those choices there are 8 possibilities for the second letter, yielding a total of 9 x 8 combinations. For each such choice there are 7 remaining choices for the third letter, giving a total of 9 x 8 x 7 combinations for the first 3 letters. And so on, all the way down to the final letter, for which there will be just one choice once the other 8 letters are chosen.
However, we don’t have 9 distinct letters – there are 6 repeats of M and 3 of B. So, each of those 9! arrangements has 6! repeats due to repetitions in the M and 3! repeats due to repetitions in the B. It follows that the number of distinct arrangements is
\frac{ 9!}{6!3!} = 84
and the probability Magnus wins 6 of the games is
\frac{ 9!}{6!3!} \times (0.4)^6 \times (0.6)^3 = 0.0743
So, the trick was to calculate the probability of Magnus winning a specific sequence of 6 games, realise that all such sequences have the same probability, and then multiply that probability by the number of different combinations.
The Eight Queens Puzzle
In some situations, it’s necessary to be a bit careful to avoid repeat counting. For example, consider the Eight Queens chess puzzle: what’s the probability that if I randomly place 8 queens on the chessboard, no two queens are attacking one another? That’s to say, no two queens lie on the same line: horizontal, vertical or diagonal.
Here’s one solution, for example:

The first part of the calculation is easy. By the same counting argument as for the previous question, the number of different ways we can place the 8 queens on the board is
\frac{ 64!}{56!8!} =4426165368
Much more difficult is finding the number of such arrangements that satisfy the condition, like the one in the figure above, that none of the queens is attacking any of the others. It turns out that there are 12 fundamental and unique solutions, as per the following diagrams:
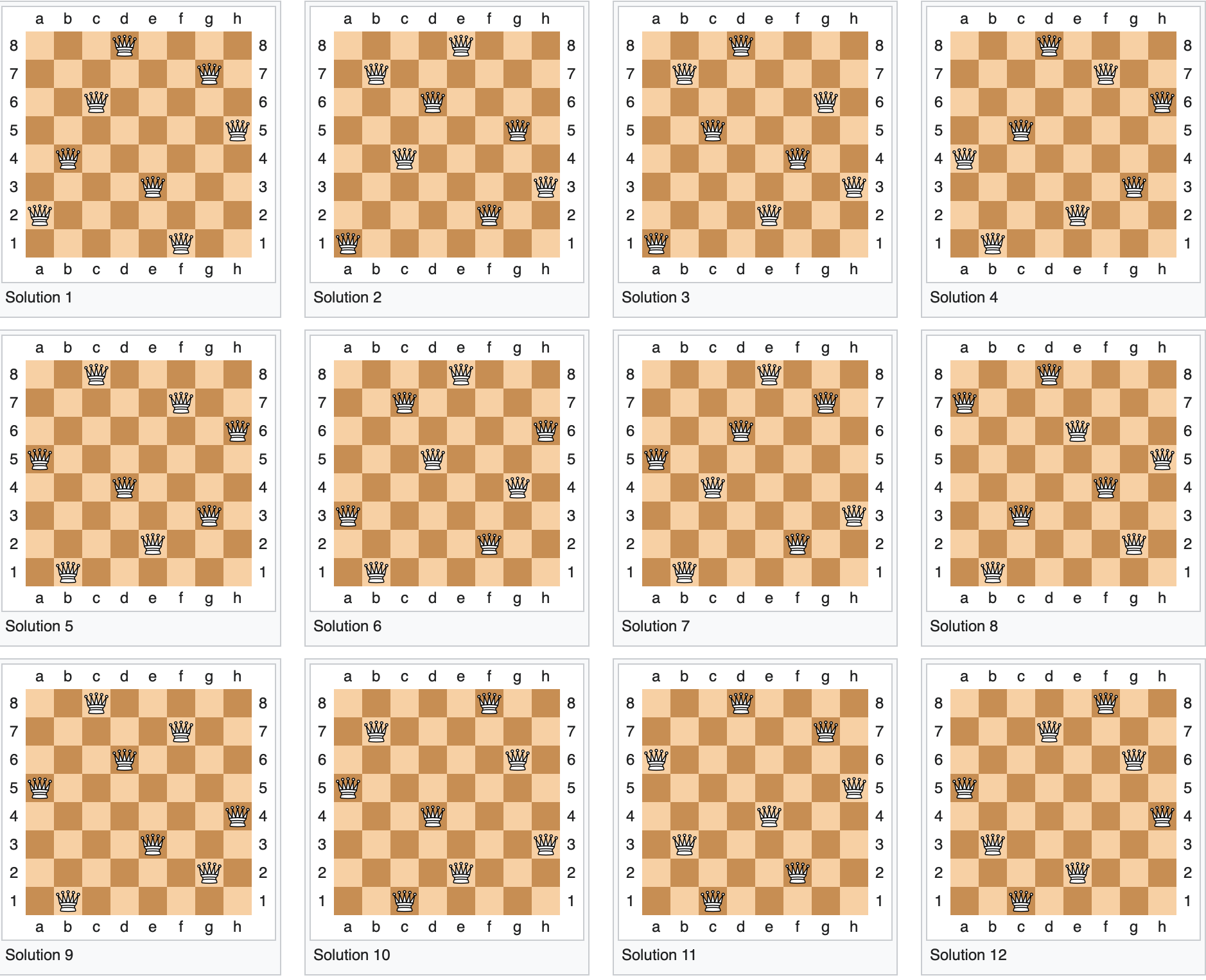
But there’s a twist. Each of solutions 1-11 can be rotated by 90, 180 or 270 degrees, yielding a ‘new’ solution that is distinct from the original one. This implies that each of these solutions actually generates four unique solutions. Moreover, each of those possibly rotated solutions can be mirror-reflected to generate another unique solution. It follows that each of the fundamental solutions 1-11 actually generates 8 different solutions, allowing for rotation and reflection. By contrast, solution 12 is already identical to itself on rotation of 180 degrees, so while each of solutions 1-11 generate 8 distinct solutions each, solution 12 generates only 4. The total number of unique solutions is therefore
11 \times 8 + 4 = 92
and the probability that a random arrangement satisfies the queens’ puzzle criterion is
\frac{92}{4426165368} \approx 2.1 \times 10^{-8}
The point is, when counting arrangements, care has to be taken to ensure that each possible arrangement is counted once and only once, and in complex situations this may require some care.
Chess 960
Another issue can be illustrated by the following chess problem. The chess variant Chess 960 was invented by world chess champion Bobby Fischer. Bored, no doubt, by winning most standard chess games he played, he suggested an alternative in which the starting positions for white’s pieces don’t necessarily follow the standard rules, but are randomised according to the following scheme:
- The pawns are placed on the second rank, as per the standard rules.
- The position of the remaining pieces are randomised on the first rank subject to the following limitations:
- The bishops must occupy squares of opposite colours. This ensures the bishops cannot clash with each other; and
- The rooks must be on opposite sides of the king. This ensures that castling on either side is still an option.
Once white’s starting position is randomised subject to these rules, black’s position is fixed to be the mirror-equivalent.
Here’s one valid arrangement, for example:
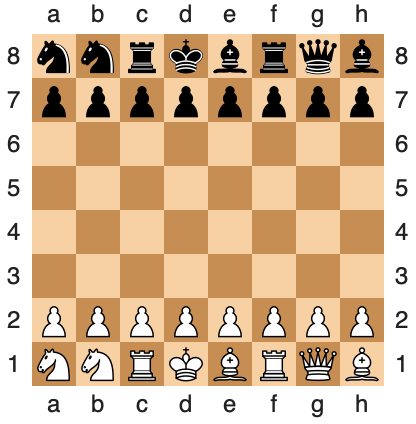
Chess 960 gets his name because there are 960 different ways of arranging the pieces on the board, subject to the rules specified above. The challenge is: can you show why 960 is the correct number of possible arrangements?
Think about it a little, then scroll down for the answer and discussion:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Start with the bishops. There are 4 options each for the black-square and white-square bishop, giving a total of 4 x 4 arrangements. For each of those, that leaves 6 spaces for the queen. Once the queen is placed, there are 5 positions left to place the 2 knights. But the the two knights are indistinguishable, so by the familiar counting argument we’ve seen above, the number of such placements for the two knights is
\frac{ 5!}{2!3!} = 10
We now have 3 places left to be filled by the king and two rooks. But this can only be done one way because of the requirement that the 2 rooks are either side of the king. The total number of possible combinations for all the white pieces is therefore
4 \times 4 \times 6 \times 10 \times 1 = 960.
Finally, since black’s pieces must mirror white’s, 960 is the total number of arrangements for the entire set.
The interesting thing here, however, is that the calculation is easy as long as you take the pieces in the order that I stated above. If you try starting from the position of the king, for example, thing become much more complicated. Just try it. There are 8 possible positions for the king, but 2 of them are ruled out by the requirement of having a rook on either side. So that’s just 6. The number of places for the rooks will then depend on the actual square you’ve chosen for the king. And once you’ve fixed the king and the rooks, the number of options for the bishops will depend on whether the rooks occupy the same colour square or not. And so on. WIth care, it can still be done, but it’s considerably more complicated.
Postscript: The Matthew Puzzle
Finally, here’s a puzzle which, although not strictly about combinations and counting, does require similar logical thinking.
You’ve got a match ticket in a small section of the Gtech Community Stadium that has 100 seats. Each ticket is assigned to a specific seat and spectators take their seat one at a time. However, one of the other 99 attendees – let’s, for argument’s sake, call him Matthew – decides to sit in a random seat selected from those that haven’t yet been occupied. All other ticket-holders will sit in their assigned seat unless it’s already taken, in which case they sit in a random seat among those still unoccupied. You are the last person in the queue to take your seat; Matthew is in some random position in front of you in the queue. What’s the probability you end up sitting in the seat to which you’ve been assigned?
If you can solve this puzzle, great; I’d love to see your solutions. But in any case, please send me (at stuart.coles1111@gmail.com) your best guess at the probability. As with previous puzzles, it’s an interesting exercise to learn how accurate our collective intuition is at problems of this type. In the next post I’ll give a couple of alternative solutions and also summarise any responses I receive.
