Introduction
This is the first of two posts discussing an experiment that I invited Smartodds employees and associates to participate in. The whole thing is rather a lot for a single post, so I’m splitting it into two. This first post will focus on theoretical aspects; in the follow-up I’ll look at what happened in practice.
The experiment is an exact replica of one that was published and subsequently reported in the Economist. It concerns betting strategies and, in particular, how much of your bank you should bet when you have a series of bets to make but only a limited amount of money to play with.
The rules of the game were as follows:
- You start with a bank of $25.
- You play a series of virtual coin tosses in each of which the probability of a Head is 60% and the probability of a Tail is 40%.
- For each coin toss, you can choose either Heads or Tails and the amount you wish to stake, in units of $0.01, up to the current bank value.
- Each bet is offered at even money: for a stake of (say) $5, you win $5 if you guess the coin correctly, otherwise you lose $5.
- The game stops if you hit $0.
- There’s also an unspecified upper limit to your bank size. The game stops if you hit this upper limit.
- The game times out after 30 minutes if you haven’t hit the upper or lower limit first.
- Your aim is to make as much money as possible.
These rules are identical to those of the published study, so it’s fair to make a comparison of results, which I’ll do in the next post. Here, I’ll focus on the question of what strategy is optimal for playing this game.
Optimal Play
At each turn in the game, the player has two choices to make: whether to call Heads or Tails, and the size of the stake.
The first of these aspects is easy to address: to optimise expected winnings the player should play Heads on every turn. It may seem intuitive to play Tails once in a while, since they will show up on around 40% of occasions. Or if you’ve had a run of Heads, it may seem like Tails is a good bet since the run of Heads is bound to end at some point. But both these intuitions are misplaced: there is a greater chance of a Head occurring on each turn, regardless of previous results, and since the reward is the same for a correct guess of either type, the amount you expect to win by playing Heads on any turn is greater than that when playing Tails.
More precisely, a unit stake bet on Heads has an expected profit of
(60% x 1) + (40% x (-1)) = 0.2
while a unit stake bet on Tails has an expected profit of
(60% x (-1)) + (40% x 1) = -0.2
These results are true regardless of the previous sequence of results, so since you’re looking to make rather than lose money, you should always bet on Heads.
But the more interesting aspect, and really the main focus of the experiment, is the choice of stake size. Let’s simplify things for now by assuming there are a fixed number of rounds and there’s no upper limit to the bank size.
One approach is to aim to maximise the amount of money you expect to win overall, which in turn implies betting your entire bank at every round. At first sight this is a totally rational paradigm, but it turns out to have a massive downside.
With a fixed number of rounds, it’s very easy to analyse what happens. Let’s consider a sequence of 10 rounds. You’re going to predict Heads every time, betting your entire bank at every round. You’ll win if every coin toss comes up Heads; but as soon as a Tail occurs, your bank reduces to zero and the game stops.
At the end of 10 rounds, assuming you get that far, if you win, you win big. You’ll have doubled your bank at every round, so:
Final bank = $25 x (2 multiplied by itself 10 times)= $25,600
But the chance of getting that result is
Probability = 0.6 multiplied by itself 10 times = 0.006
Any other outcome will result in a final bank of zero, which therefore occurs with probability 0.994.
It follows that the average final bank is
Average final bank = ($25,600 x 0.006) + ($0 x 0.994) = $154.79,
which is the best possible average across all staking strategies.
However, according to the above calculations, when using this strategy you’ll end up with $0 on more than 99% of occasions. And that’s with just 10 rounds of the game. With more and more rounds, the probability of avoiding $0 becomes vanishingly small.
What’s happening is that expected wealth is maximised with a strategy that will almost always result in you losing the entire bank. Very, very occasionally you’ll win a lot of money – but almost always you’ll end up with nothing. In fact, if you play the game for an unlimited number of rounds, with probability 1 you will end up with $0; this is the well-known St. Petersburg Paradox.
So, unfortunately, the approach of aiming to maximise your average winnings, which implies betting your entire bank at every round, also means accepting a very high probability of ending up with $0.
Be Happy
This dichotomy can be avoided by relating money to Happiness. Winning money makes you happy, losing money makes you unhappy, but you can choose the precise way in which winning or losing money affects your Happiness. You might decide that winning and losing $5, say, makes you equally happy and unhappy. Alternatively, you might decide that losing $5 causes you to be more unhappy than winning $5 and that the less money you have, the worse you’ll feel about losing $5.
These two alternatives – Linear and Logarithm Happiness, respectively – are shown in the following graphs:
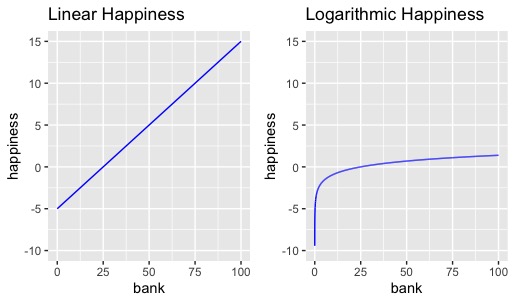
In both cases, the more money I have, the happier I am, but in other respects the relationship between Happiness and money is quite different. With Linear Happiness, losing a certain amount of money leads to an increase in Happiness that’s equal to the decrease in Happiness when I lose the same amount of money. For example, whenever my bank increases by $5, my Happiness increases by 1; whenever my bank decreases by $5, my Happiness decreases by 1. But with Logarithmic Happiness, losing and winning the same amount have different effects on my Happiness. If I have $25, an increase of $5 increases my Happiness by 0.18, but a loss of $5 decreases my Happiness by 0.22. And this difference is exaggerated if I have less money to begin with: if I start with $10, a gain of $5 will increase my Happiness by 0.41, but a loss of $5 will decrease it by 0.69.
Now, a reasonable system for setting stake sizes is to aim to maximise expected Happiness, but this leads to different strategies depending on the choice of relationship between Happiness and bank size. In the Linear Happiness case, Happiness is proportional to bank size, so maximising expected Happiness is equivalent to maximising the expected bank, leading to the ‘bet-the-entire-bank-every-bet’ strategy discussed above. But using Logarithmic Happiness, strategies that are likely to result in a bank close to $0 are heavily penalised, resulting in a system known as the Kelly Criterion:
- The Kelly criterion requires betting a fixed proportion of your bank at every round. This means your stake size is dynamic, changing from round to round. But it only depends on the current value of your bank, not, for example, whether you won or lost in the previous round.
- The actual proportion of your bank that you should bet each round depends on the price of the bet and the probability of winning according to the following formula:
proportion = win probability – (1- win probability)/(price – 1)
- In this example, the price of the bet is 2 – that’s the amount you get back, including the stake, if a unit stake bet wins – and the probability of winning is 60%. This formula therefore implies you should always bet exactly 20% of your current stake. Since you start with $25, this means the first bet should be placed at a stake of $5. If it wins, your bank is then $30, and your next bet should be placed with a stake of $6. If it loses, your bank is $20, and your next bet should be placed with a stake of $4. And so on.
The reasoning behind betting a constant proportion of the bank – if not the value of the proportion – is intuitive. First, betting this way – as long as you ignore the rounding issue – means you will never hit zero, since you never bet the entire bank. Second, the solution should be unit-free: you would expect the strategy to be the same regardless of whether you start with $25 or $25 million, for example. It really wouldn’t make sense to bet $5 in both cases. Betting a constant proportion of the current bank gets round this problem.
Why the actual proportion should be determined by the Kelly formula is a little more technical – see the Wikipedia article for details – but the idea is simple enough. Kelly’s formula provides the value of the proportion to stake which leads to the maximum improvement in Happiness per bet. For example, with a win probability of 60% and a price of evens, as per the game settings above, the following plot shows the average change in Happiness per bet for different values of the staking proportion:
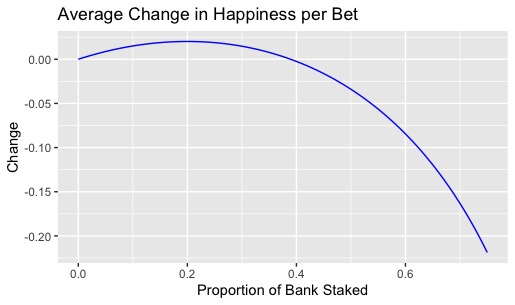
You can see that the maximum increase per bet in expected Happiness (of around 0.02) does indeed occur when a fraction 0.2 of the bank is staked. Moreover, any choice of fraction between 0 and around 0.38 will result in an increase in average Happiness. By contrast, fractional bets greater than 0.38 result in a reduction of expected Happiness. If the curve were extrapolated further, you’d see that betting the whole bank every time – that’s to say, using a fraction of 1 – would lead to a very big drop in expected Happiness on every bet: formally, I’d be infinitely unhappy on average.
The difference in practice between using the Kelly criterion and betting the entire bank on each bet is clearly seen in the following histograms.
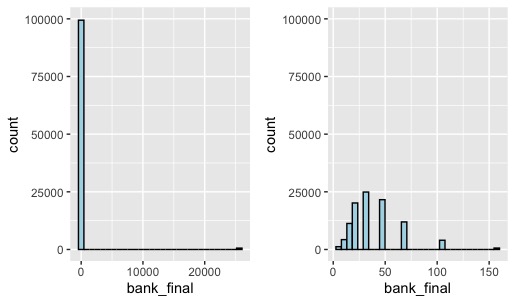
In each case, I’ve simulated 10 rounds of the game (without the upper limit on the bank size) 100,000 times. The left-hand plot shows the counts of different final bank totals when always betting the entire bank; the right-hand plot shows similar results when using the Kelly criterion for stake sizes. As explained above, what happens in the first case is that you almost always end up with $0, compensated by the fact that you very occasionally win very big. (Notice the count is slightly greater than 0 for a value of around $25,000; actually, $25,600 as explained above). The average final bank in this case turned out to be $150, very close to the theoretical value of $154.79 calculated above.
Using the Kelly criterion things are very different. The average final bank is a lot lower, at around $37. Furthermore, the maximum value of the final bank, which also occurs infrequently, is much lower at just over $150. So, Kelly leads to lower average winnings and a much lower maximum possible win. On the other hand, you’ll never end up with $0, and in most cases not even close to $0. Indeed, with Kelly the final bank is greater than the initial value of $25 on around 63% of occasions; with the all-in betting strategy it was only 0.6%. And this is with just 10 rounds of the game – with more rounds, the differences in results when using the different strategies become magnified.
So: do you want to take your chances and win a lot of money with vanishingly small probability? Or, do you want to be reasonably certain of winning something and be pretty well protected from losing a large proportion of your bank, even if your average win is lower? By and large, it’s commonly accepted that the latter aim is preferable, and the Kelly criterion, or some variant of it, is widely adopted in both betting and investment circles. Nonetheless, if you could play this game a virtually unlimited number of times, you’d make a lot more money with the ‘bet-the-entire-bank-every-bet’ strategy than with Kelly.
Why “Optimal” Might Not Be Optimal
Leaving aside the precise details of the Kelly criterion, there are two reasons why the theory doesn’t apply exactly for the game described above. The first is due to the fact that bets can only be placed in units of $0.01. For example, if your bank gets as low as $0.01, you can only bet the whole bank, and not the 20% that Kelly would require.
The second, more important, reason is that there’s an upper limit to the amount that can be won. This is easier to understand when the upper is known to players. For example, suppose your current bank is $249 and you know the upper limit is $250, which is the actual value in this game. Then you’d know there is no point betting more than $1, whereas the Kelly criterion would require you to bet 20% of $249.
The fact that the limit is unknown complicates things. Is not knowing the limit equivalent to there not being a limit? Does the Kelly criterion still apply? If so, is the 20% proportion still valid? If not, how should things change? I don’t know the answers here, which is one reason why the experiment is interesting and informative, even among players who know what the Kelly criterion is and how to implement it.
Finally, apart from the choice of bet (Heads/Tails) and stake size, there is one other aspect of the game that players have some control over, and that’s the number of bets placed. Intuitively (and correctly), since bets on Heads have positive value, players should aim to make as many bets as possible, subject to the time and upper/lower bank limits. Moreover, knowing that there’s an upper limit to the bank size, it might be reasonable to reduce risk by placing stakes at a lower level than Kelly implies, but aiming to make more bets by betting at a faster rate.
Summary
In summary, theoretical arguments based on the Kelly criterion suggest a player should:
- Always bet Heads.
- Bet a constant proportion of the bank at each round.
- Never adjust stake size on the basis of the actual sequence of Heads and Tails observed, except in so much as they determine the size of the current bank.
- Stake a proportion of the bank that’s something like 20%.
- Make bets as quickly as possible.
The specifics of the game rules, such as the limit to the bank size, mean that some of these guidelines may not be exactly optimal, but something along these lines is likely to be a reasonable strategy in any case.
In the follow-up post I’ll summarise the different strategies that different participants adopted and the outcomes they led to. I’ll also compare strategies and results with those reported in the original published study.
Postscript: an anecdote.
In the early days of Smartodds, I was involved in a discussion with Matthew Benham and others about staking strategies. Matthew’s reply when asked about his strategy was “AMAP” (As Much As Possible). In other words, forget Kelly, just place the most you can on every single bet.
But this is less incompatible with Kelly than it first seems. In practice, AMAP isn’t the same as “The Whole Bank” since stake sizes are always limited by the amount a bookmaker is willing to match. And without wishing to speculate on the size of Mr Benham’s bank, it’s likely that AMAP, because of bookmaker limits, is actually less than the amount that would be implied by Kelly. In other words, AMAP is probably less than optimal, not because it implies betting too much of the bank, but because bookmaker limits force you to bet too little. This being so, another way of looking at things is that AMAP is as close to Kelly as you can get, given that bookmakers are prohibiting you from doing the real thing.
