A common theme to the posts in this blog is that Statistics and statistical thinking have applications that are many and varied. Usually, in one way or another, things comes down to the analysis of data – perhaps to get an understanding of the process behind those data; perhaps in order to make predictions for similar future events. But Statistics is also at the heart of many problem-solving algorithms that have nothing to do with data analysis.
For example…
Everyone plays Wordle these days. But in case you don’t, it’s like a cross between Hangman and Mastermind. Once a day a unique 5-letter key word is chosen by Wordle and your task is to identify it. You get up to 6 guesses, and after each turn your guess is analysed for its accuracy. Letters in your guess that are in the correct place are highlighted as such (with a green square), while letters that are present in the key word but in the wrong place are also highlighted (by a yellow square).
To illustrate, suppose the hidden key word is POINT and my first guess is STING. Then, Wordle’s analysis would be that I and N are in the correct place, while T is also correct but in the wrong place.
In my second turn I’ll use that information when making my next guess. If I guess correctly, then I’ll have solved the puzzle in 2 turns. If not, then I’ll get the analysis for this new guess, which I can then use to make a better guess in the next turn. If the puzzle isn’t solved within 6 turns then I’m timed out. And one unique aspect of Wordle that adds to its appeal is that there’s only one gameplay per day. Win or lose, you have to wait till the next day to play again with a new word to guess.
Here’s another example showing the Wordle interface.

My first guess was SANER. The yellow tile is Wordle telling me that the key word contains the letter N, but not in that place. The remaining letters in SANER are all grey, meaning they are not present in the key word. My second guess, which is consistent with that information, is COUNT. The green tiles in this case correspond to Wordle’s analysis that O, U, N and T are correctly placed in the key word, while C can be excluded, together with the excluded letters from my first attempt. My third guess was MOUNT, and the full row of green tiles implies this is the correct answer. I therefore solved the puzzle in 3 rounds.
So, the rules of Wordle are simple enough. But like most games, playing is one thing; playing well is something else. But what does it mean to play Wordle well? Is there an optimal strategy? And what does optimal even mean?
As usual, you might like to think about these questions before reading on.
|
|
|
|
|
|
|
|
|
|
Here’s one approach.
Imagine a bag containing all possible 5-letter words. Once I’ve made a guess, and been given Wordle’s analysis in reply, some – perhaps many – of those words will no longer be admissible solutions, and I can remove them from the bag. Returning to the first example above, if I tried STING when the hidden word was POINT, then with the information that I and N are in the right place, and T is also included but not where I guessed, the words THINK, PAINT, POINT and FAINT (amongst others) are still admissible and would remain in the bag. Other words like FLARE, RACES, CHASE and TREES (as well as many others) would be incompatible and could be removed from the bag.
So, was STING a good choice? Well, we’re trying to home in on the hidden word, removing all words that are inadmissible after each new piece of information provided to me by Wordle. If the bag contains many words my task is more difficult, as I’ll have more options to choose from next round. That means I’m trying to empty the bag as quickly as possible, and STING will have been a good choice if the analysis it resulted in meant I could remove many words from the bag.
Ideally, after making a guess, the bag will be empty, since I’ll already have found the solution and no other words will be admissible. The next best thing would be if the bag contained just one word, since that must be the only admissible word remaining, so if I use that word as my next guess it must be the correct solution. More generally, the fewer the words in the bag the better, since then I will have fewer admissible words to choose from in the next round.
This all means that we can judge the quality of a guess by the number of words it leaves in the bag after making that choice and receiving the analysis from Wordle. Unfortunately, to know how many words will be left after my choice of STING, or any other word, I’d have to know what the key word is. So that’s not an option. But in principle, at least, I could work out how many words will be left in the bag after making my guess for every currently admissible choice of key word – that’s to say, for every single word still in the bag. Then, assuming that all words in the bag are equally likely to be the key word, I can use the average of those scores as a measure of how good the choice STING is. If I repeat this calculation for all remaining admissible words, I’ll have a measure of how good each admissible guess is, and can choose to make the one that has the best (lowest) score.
Let’s look at a simpler example. Suppose we’re playing Wordle but with 3-letter words, and the only words available are CAT, COT, DOT, AND, TIP. Then it’s not too difficult to build the following score matrix:

The rows are the words that I could choose for my first turn; the columns are the possibilities for the key word, which is unknown to me. The values in the matrix count how many words will remain in the bag at the next turn if I make a particular choice (as given by the row name), when the key word happens to be that of the column name. As an example, suppose I choose the word AND. Then if CAT happens to be the key word, the analysis will be that I have no letters in the correct place, but A in the wrong place. The only word satisfying that criterion is CAT and therefore only 1 word (CAT) remains in the bag for my next choice. On the other hand, if COT is the true word then the analysis when choosing CAT will be C and T in the correct place, and no other letters correct, in which case 2 possible words remain – CAT and COT – for the next round. In this way the score matrix shows how many words are left in the bag for every combination of guess and key word. The diagonal elements are all zero since they correspond to me guessing correctly the key word, so no words would remain in the bag after that choice.
In themselves these scores aren’t useful, since we never know the key word until the puzzle is solved. Which leads to the statistical part of the solution. Though we can’t calculate the actual guess/key-word score, since we don’t know the key word, we can calculate the average score across all possible key words. This will give us a measure of the quality of the guess in absence of knowledge of the key word, other than that the key word has to be one of those currently admissible.
So, returning to the 3-letter word example, we average the scores across the columns, leaving an average score per row which corresponds to the average number of admissible words that will be left after analysis if I use as my guess the word for that particular row:
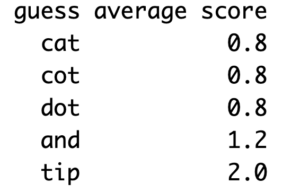
On this basis CAT, COT and DOT are all equally good guesses, since on average (across all possible choices of the key word) there will be 0.8 words left in the bag at the next round. By contrast, TIP is the worst choice since, on average, there will still be 2 words left in the bag at the next round. My optimal choice at this round is therefore any of CAT, COT or DOT, and I can select randomly between these options. Once I make my guess and get Wordle’s analysis, I’ll have either solved the puzzle, or if there is more than one word remaining, I can remove the inadmissible words and apply this procedure again to find the optimal choice for the next round.
In summary, at each round:
- I have a conceptual bag containing admissible solutions;
- For each of those words I calculate a score, which is the average number of words that remain admissible if I choose that word as my guess, where the average is taken with each admissible word as the key word in turn;
- I’ll make my guess the word with the lowest score, using randomisation to break ties if necessary;
- I obtain the analysis from Worlde based on my optimised guess;
- The analysis is either that my guess is the key word, in which case I can stop, or I can use the analysis to remove further inadmissible words from the bag, and then go back to 1. for the next round.
To enable this procedure for the full-scale 5-letter Wordle, I first downloaded a dictionary of 5757 5-letter words. This is my complete bag of words that I’m assuming to contain all possible solutions to Wordle when I have no information. I then applied the procedure described above to construct a 5757-by-5757 matrix of scores, for each guess-true word pairing, which I then averaged row-wise to get an average score for each possible guess. That’s to say, I applied exactly the same procedure as above, but with a dictionary of 5757 words instead of just 5.
The optimal initial guess is then the word with the smallest average score. This happens to be TARES, which though obscure, is a genuine English word. TARES has an average score of just 132.5 words going forward to the second round. There’s also independent evidence that this is indeed the optimal choice. For reference, the worst choice in my dictionary is OHHHH, which would lead to an average score of 2477.3 words remaining in the second round. (Quite possibly OHHHH isn’t a valid word so far as Wordle is concerned either, but that’s a different issue).
Based on Wordle’s analysis of TARES – or whatever alternative I choose in the first round – I’ll be left with a set of N admissible words for the second round – these are the words still in the bag after I’ve removed those that are incompatible with Wordle’s analysis of my first guess. I then create the N-by-N sub-matrix of all possible guess/key-word scores, and use that to get the average scores based on the remaining admissible words. The optimal next guess is then the word with the smallest score. This procedure then repeats until I’ve found the correct word.
This all sounds complicated, but I only had to do the hard work once, calculating the Wordle analysis for every one of the 5757-by-5757 combinations of guess and key word. Once this is done, and stored, I can reduce it to the relevant set of N-by-N admissible word pairs at any round. And from there it’s easy to calculate the score matrix and then average scores for each currently admissible word, as illustrated above in the 3-letter word example. After the one-off initial calculation which takes several hours, the algorithmic selection of the optimal guess, round by round, followed by elimination of the inadmissible words is almost instantaneous.
With fairly rudimentary programming skills I was able to program this algorithm reasonably comfortably in R. If you have a gitlab account you can download the functions, dictionary and corresponding matrix of Wordle analyses here, though you’ll also need access to R to run things. A README file explains all the details.
It would be straightforward to assess the performance of the algorithm by evaluating how many attempts are required to find the missing word for every possible key word in the dictionary. I haven’t done that, but I have used the algorithm – with some small variations, as discussed below – to solve the puzzle daily for a few months. At the time of writing, the performance is summarised in the following output, also supplied by Wordle.
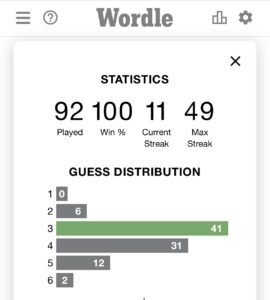
This shows I found the solution in 6 or fewer attempts every day that I played. The most frequent number of attempts required is 3 and I only needed to use the maximum number of 6 attempts on two occasions. The current streak length is quite short, but only because I forgot to do the puzzle on a few occasions. My average number of attempts based on this information is 3.6, which is slightly better than Sweden’s, the country with the best average. (I have some doubts about the reliability of the average scores reported in this article, however).
Some additional points…
- When calculating the average score for admissible words as described above, the algorithm assumes that all admissible words are equally likely. This is likely not to be true – the words chosen by Wordle are generally not obscure (though the key word was CAULK recently, which set off a bit of a fire on Wordle Twitter). This means that someone not using this algorithm, but choosing words that are more common – and therefore more likely to be the solution – may get better results. The algorithm itself could be modified to account for this possibility. Rather than just calculating the average of the scores, we could use a weighted average, giving more weight to words that we regard as more likely solutions, perhaps based on standard libraries of word usage. This would lead to the algorithm, on average, finding the solution in a smaller number of steps as long as the weights correspond well to the relative likelihood of Wordle picking these words.
- The algorithm can only find words that are included in the sample dictionary – in my case, the set of 5757 words that I downloaded. If Wordle chooses a word outside of this set, the algorithm can’t possibly find it. Equally, though less seriously, it’s possible that the dictionary I downloaded includes words that Wordle doesn’t recognise. Actually, I know this to be the case, since at times when playing the game the algorithm has selected a word which is actually rejected by Wordle as being unrecognised. It’s likely that OHHHH falls into this category. The algorithm will still work in this case, but will be less efficient, since the calculation of the average scores will include scores based on irrelevant words.
- The algorithm isn’t necessarily optimal in the sense of minimising the total number of guesses required to find the key word, since it only looks ahead to the next round. For example, suppose we try the word SHARE as a first guess and find that S, H, A and E are in the correct place, but R is wrong. Based on this information the missing letter could be any of D, K, L, M, P, or V. The algorithm would give equal score to each of the words SHADE, SHAKE, SHALE and so on, so the optimal guess would be any of these choices, which might as well be chosen at random. If the word I choose is correct, I’m done. But if it’s wrong, it doesn’t eliminate any of the other admissible choices. It’s possible, therefore, that I would need a further 6 rounds to complete the game – implying a total of 7 – and I’d be timed out. In this case it might be better to choose a word that would potentially eliminate several letters, even if that word can’t possibly be correct. For example, PLUMB can’t possibly be correct, since it’s inconsistent with the information from the previous round, but from the information I get back from Wordle by making this choice I will know whether the true word contains any of P, L or M. So, although I am effectively ‘wasting’ a turn, the information I get might help me reduce the average number of overall turns needed.
- It’s not necessary when using the algorithm to make the optimal choice in each round. For example, as a first guess one might adopt the second best choice – RATES, with a score of 135.8 – rather than TARES. Though strictly sub-optimal, by the criterion defined within the algorithm, it might nonetheless be a better choice for two reasons. First, as discussed above, Wordle seems to avoid unusual words like TARES; second, because whoever chooses the key words for Wordle, knowing that TARES is the optimal first guess, might avoid words that are good second guesses after using TARES as a first guess.
- There is a belief that Wordle is becoming more difficult, especially since it was recently bought by the New York Times. This could happen in either of two ways. Either, the selected word could become more obscure (e.g. CAULK). Or, the word could be similar to many other words (e.g. SHARE as discussed above).
- The algorithm described above is neither mine nor novel. It’s actually the analogue of an algorithm proposed by Donald Knuth to play Mastermind. This isn’t the only possible statistical approach to playing Wordle. For example, this article describes a simulation-based method which is comparable in performance to the Knuth algorithm, so long as the initial guess is chosen carefully.
Finally, bored of Wordle? How about Quordle, Nerdle, Worldle, Crosswordle, Taylordle, Sweardle…
